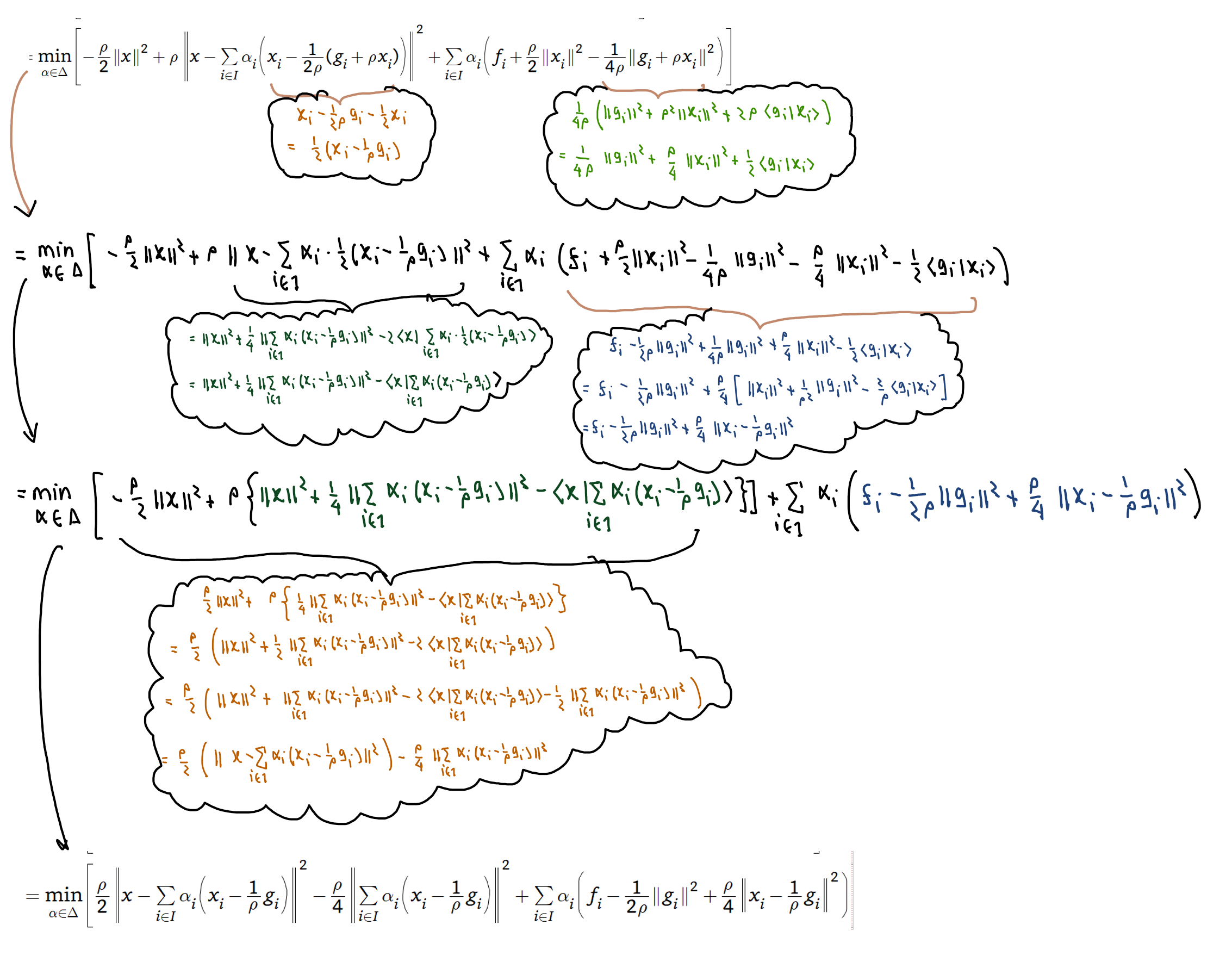Properties of smooth nonconvex interpolated functions

Shuvomoy Das Gupta

November 24, 2021

In this blog, we study properties of $\rho$ -smooth nonconvex function that is interpolated from a set of points. This result is due to Yoel Drori and Ohad Shamir from [1, Theorem 7].

Table of contents

Notation and notions
A few helper results
Main result
References

Notation and notions

All norms are 2-norm in this blog.

A differentiable function $f:\mathbf{R}^{d}\to\mathbf{R}$ is $L$ -smooth convex if and only

\left(\forall x,y\in\mathbf{R}^{d}\right)\quad f(y)\geq f(x)+\langle\nabla f(x)\mid y-x\rangle+\frac{1}{2L}\|\nabla f(x)-\nabla f(y)\|^{2}.

A differentiable function $f:\mathbf{R}^{d}\to\mathbf{R}$ is $\rho$ -smooth nonconvex if and only if

\left(\forall x,y\in\mathbf{R}^{d}\right)\quad-\frac{\rho}{2}\|x-y\|^{2}\leq f(x)+\left\langle \nabla f(x)\mid y-x\right\rangle -f(y)\leq\frac{\rho}{2}\|x-y\|^{2}.

The set of all $L$ -smooth convex functions on $\mathbf{R}^{d}$ is denoted by $\mathcal{F}_{0,L}(\mathbf{R}^{d})$ and the set of all $\rho$ -smooth nonconvex functions is denoted by $\mathcal{F}_{-\rho,\rho}(\mathbf{R}^{d})$ .

A few helper results

We first record the following result from [3, Lemma 2.53].

Relationship between smooth convex and nonconvex functions

Lemma 1: Relation between smooth convex and nonconvex functions.
Lemma

For any

f:\mathbf{R}^{d}\to\mathbf{R}

, we have

f\in\mathcal{F}_{-\rho,\rho}(\mathbf{R}^{d})\Leftrightarrow f+\frac{\rho}{2}\|\cdot\|^{2}\in\mathcal{F}_{0,2\rho}(\mathbf{R}^{d}).

Interpolable function

Next, we present the definition of an interpolable function.

Definition 1: Interpolable function.
Definition

Suppose we are given the set of triplets

\{(x_{i},g_{i},f_{i})\}_{i\in I}

where

I

is a finite index set and

x_{i}\in\mathbf{R}^{d},g_{i}\in\mathbf{R}^{d},

and

f_{i}\in\mathbf{R}.

Let

\mathcal{F}(\mathbf{R}^{d})

be a set of functions on

\mathbf{R}^{d}

. Then the set

\{(x_{i},g_{i},f_{i})\}_{i\in I}

\mathcal{F}(\mathbf{R}^{d})

-interpolable if and only if there exists a function

f\in\mathcal{F}(\mathbf{R}^{d})

such that for all

i\in I

we have

f_{i}=f(x_{i})

and

g_{i} \in \partial f(x_{i})

. We say that

f\in\mathcal{F}(\mathbf{R}^{d})

is an interpolated function that interpolates the set

\{(x_{i},g_{i},f_{i})\}_{i\in I}

Interpolation condition for smooth nonconvex functions

Next, we record the following result that follows from [1, Theorem 3.10] regarding interpolated functions on $\mathcal{F}_{-\rho,\rho}(\mathbf{R}^{d})$ . Note that, the published version of the paper [1] contains a typo in this theorem, which is corrected in a subsequent arxiv update available at https://arxiv.org/pdf/1512.07516.pdf.

Theorem 1: Interpolation condition for smooth nonconvex functions.
Theorem

Let

\rho>0

, and consider the set of triplets

\{(x_{i},g_{i},f_{i})\}_{i\in I}

, where

I

is a finite index set. Then

\{(x_{i},g_{i},f_{i})\}_{i\in I}

\mathcal{F}_{-\rho,\rho}

interpolable if and only if for all

i,j\in I

we have

f_{i}\geq f_{j}+\left\langle g_{j}\mid x_{i}-x_{j}\right\rangle +\frac{1}{2\rho}\|g_{i}-g_{j}\|^{2}-\frac{\rho}{4}\left\Vert (x_{i}-x_{j})-\frac{1}{\rho}(g_{i}-g_{j})\right\Vert ^{2}.

Proof.

Suppose, for all $i,j\in I$ we have

\begin{aligned} & f_{i}\geq f_{j}+\left\langle g_{j}\mid x_{i}-x_{j}\right\rangle +\frac{1}{2\rho}\|g_{i}-g_{j}\|^{2}-\frac{\rho}{4}\left\Vert (x_{i}-x_{j})-\frac{1}{\rho}(g_{i}-g_{j})\right\Vert ^{2}\\ \Leftrightarrow & f_{i}\geq f_{j}+\left\langle g_{j}\mid x_{i}-x_{j}\right\rangle +\frac{1}{2\rho}\|g_{i}-g_{j}\|^{2}-\frac{\rho}{4}\left(\|x_{i}-x_{j}\|^{2}+\frac{1}{\rho^{2}}\|g_{i}-g_{j}\|^{2}-2\frac{1}{\rho}\left\langle x_{i}-x_{j}\mid g_{i}-g_{j}\right\rangle \right)\\ \Leftrightarrow & f_{i}\geq f_{j}+\left\langle g_{j}\mid x_{i}-x_{j}\right\rangle +\frac{1}{2\rho}\|g_{i}-g_{j}\|^{2}-\frac{\rho}{4}\|x_{i}-x_{j}\|^{2}-\frac{\cancel{\rho}}{4}\frac{1}{\cancel{\rho^{2}}\rho}\|g_{i}-g_{j}\|^{2}+\frac{\cancel{2\rho}}{\cancel{4\rho}2}\left\langle x_{i}-x_{j}\mid g_{i}-g_{j}\right\rangle \\ \Leftrightarrow & f_{i}\geq f_{j}+\left\langle g_{j}\mid x_{i}-x_{j}\right\rangle +\frac{1}{2\rho}\|g_{i}-g_{j}\|^{2}-\frac{\rho}{4}\|x_{i}-x_{j}\|^{2}-\frac{1}{4\rho}\|g_{i}-g_{j}\|^{2}+\frac{1}{2}\left\langle g_{i}-g_{j}\mid x_{i}-x_{j}\right\rangle \\ \Leftrightarrow & f_{i}\geq f_{j}+\left\langle g_{j}+\frac{1}{2}g_{i}-\frac{1}{2}g_{j}\mid x_{i}-x_{j}\right\rangle +\frac{1}{4\rho}\|g_{i}-g_{j}\|^{2}-\frac{\rho}{4}\|x_{i}-x_{j}\|^{2}\\ \Leftrightarrow & f_{i}\geq f_{j}+\left\langle \frac{1}{2}g_{j}+\frac{1}{2}g_{i}\mid x_{i}-x_{j}\right\rangle +\frac{1}{4\rho}\|g_{i}-g_{j}\|^{2}-\frac{\rho}{4}\|x_{i}-x_{j}\|^{2}\\ \Leftrightarrow & f_{i}\geq f_{j}+\frac{1}{2}\left\langle g_{i}+g_{j}\mid x_{i}-x_{j}\right\rangle +\frac{1}{4\rho}\|g_{i}-g_{j}\|^{2}-\frac{\rho}{4}\|x_{i}-x_{j}\|^{2}.\quad\quad\quad(1)\end{aligned}

But from [1, Theorem 3.10], we have: $\{(x_{i},g_{i},f_{i})\}_{i\in I}$ is $\mathcal{F}_{-\rho,\rho}$ interpolable if and only if for all $i,j\in I$ we have

f_{i}\geq f_{j}+\frac{1}{2}\left\langle g_{i}+g_{j}\mid x_{i}-x_{j}\right\rangle +\frac{1}{4\rho}\|g_{i}-g_{j}\|^{2}-\frac{\rho}{4}\|x_{i}-x_{j}\|^{2}.

Using this along with (1) completes the proof.

■

Minimal curvature addition and interpolation

Next, we have the following equivalence in interpolation conditions between functions in $\mathcal{F}_{0,2\rho}(\mathbf{R}^{d})$ and $\mathcal{F}_{-\rho,\rho}(\mathbf{R}^{d})$ via adding minimal curvature addition to the later function class.

Theorem 2: Minimal curvature addition and interpolation.
Theorem

Consider a set of triplets

\{(x_{i},g_{i},f_{i})\}_{i\in I}\subseteq\mathbf{R}^{d}\times\mathbf{R}^{d}\times\mathbf{R}

and let

\rho>0

. Then the following are equivalent.

(i) $\{(x_{i},g_{i},f_{i})\}_{i\in I}$ is $\mathcal{F}_{-\rho,\rho}(\mathbf{R}^{d})$ -interpolable.

(ii) $\{(x_{i},g_{i}+\rho x_{i},f_{i}+\frac{\rho}{2}\|x_{i}\|^{2})\}_{i\in I}$ is $\mathcal{F}_{0,2\rho}(\mathbf{R}^{d})$ -interpolable.

Proof.

The proof to $(i)\Rightarrow(ii)$ : It follows from Lemma 1 that if there exists a function $f\in\mathcal{F}_{-\rho,\rho}(\mathbf{R}^{d})$ interpolating the set $\{(x_{i},g_{i},f_{i})\}_{i\in I}$ , then $h\coloneqq f+(\rho/2)\|\cdot\|^{2}$ would satisfy $h\in\mathcal{F}_{0,2\rho}(\mathbf{R}^{d})$ and for all $i\in I$ we would have

h(x_{i})=f(x_{i})+\frac{\rho}{2}\|x_{i}\|^{2}=f_{i}+\frac{\rho}{2}\|x_{i}\|^{2},

and

\nabla h(x_{i})=\nabla f(x_{i})+\rho x_{i}=g_{i}+\rho x_{i}.

Hence, the set $\{(x_{i},g_{i}+\rho x_{i},f_{i}+(\rho/2)\|x_{i}\|^{2})\}_{i\in I}$ is interpolated by the function $h\in\mathcal{F}_{0,2\rho}(\mathbf{R}^{d})$ .

The proof to $(ii)\Rightarrow(i)$ : If $\{(x_{i},g_{i}+\rho x_{i},f_{i}+\frac{\rho}{2}\|x_{i}\|^{2})\}_{i\in I}$ is $\mathcal{F}_{0,2\rho}(\mathbf{R}^{d})$ -interpolable, then there exists a $h\in\mathcal{F}_{0,2\rho}(\mathbf{R}^{d})$ , such that for all $i\in I$ we would have

\begin{aligned} h(x_{i}) & =f_{i}+\frac{\rho}{2}\|x_{i}\|^{2}\\ \Leftrightarrow & f_{i}=h(x_{i})-\frac{\rho}{2}\|x_{i}\|^{2}\end{aligned}

and

\begin{aligned} \nabla h(x_{i}) & =\nabla f(x_{i})+\rho x_{i}=g_{i}+\rho x_{i}\\ \Leftrightarrow & g_{i}=\nabla h(x_{i})-\rho x_{i}.\end{aligned}

So, from the last two equations, we see that $f\coloneqq h-(\rho/2)\|\cdot\|^{2}\in\mathcal{F}_{-\rho,\rho}(\mathbf{R}^{d})$ interpolates $\{(x_{i},g_{i},f_{i})\}_{i\in I}$ . So, $\{(x_{i},g_{i},f_{i})\}_{i\in I}$ is $\mathcal{F}_{-\rho,\rho}(\mathbf{R}^{d})$ -interpolable.

■

Interpolation of smooth convex functions due to Yoel Drori

Finally, we present the following interpolation result due to Yoel Drori from [4]. I showed a detailed proof of this result in the previous blog post: here.

Theorem 3: Interpolation of smooth convex functions.
Theorem

\{(\widetilde{x}_{i},\widetilde{g}_{i},\widetilde{f}_{i})\}_{i\in I}\subseteq\mathbf{R}^{d}\times\mathbf{R}^{d}\times\mathbf{R}

\mathcal{F}_{0,L}(\mathbf{R}^{d})

-interpolable with

L>0

, then one interpolated function

\widetilde{f}\in\mathcal{F}_{0,L}(\mathbf{R}^{d})

that interpolates

\{(\widetilde{x}_{i},\widetilde{g}_{i},\widetilde{f}_{i})\}_{i\in I}

is:

\widetilde{f}(y)=\min_{\alpha\in\Delta}\left[\frac{L}{2}\|y-\sum_{i\in I}\alpha_{i}\left(\widetilde{x}_{i}-\frac{1}{L}\widetilde{g}_{i}\right)\|^{2}+\sum_{i\in I}\alpha_{i}\left(\widetilde{f}_{i}-\frac{1}{2L}\|\widetilde{g}_{i}\|^{2}\right)\right],

where $\Delta=\{\beta\in\mathbf{R}^{\vert I\vert}\mid\beta\geq0,\sum_{i\in I}\beta_{i}=1\}.$

Main result

Now we are in a position to state our main result due to Yoel Drori and Ohad Shamir from [1, Theorem 7] followed by its proof.

Theorem 4: Properties of interpolated function for smooth nonconvex function class
Theorem

Let the set

\{(x_{i},g_{i},f_{i})\}_{i\in I}\subseteq\mathbf{R}^{d}\times\mathbf{R}^{d}\times\mathbf{R}

\mathcal{F}_{-\rho,\rho}(\mathbf{R}^{d})

-interpolable, where

L>0

and

I

is a finite index set. Define:

i^{\star}\in\underset{i\in I}{\textrm{argmin}}\{f_{i}-\frac{1}{2\rho}\|g_{i}\|^{2}\},

hence,

f_{i^{\star}}-\frac{1}{2\rho}\|g_{i^{\star}}\|^{2}=\min_{i\in I}\{f_{i}-\frac{1}{2\rho}\|g_{i}\|^{2}\}.

Then the following are equivalent.

(i) The set of triplets $\{(x_{i},g_{i},f_{i})\}_{i\in I}$ is $\mathcal{F}_{-\rho,\rho}(\mathbf{R}^{d})$ -interpolable.

(ii) There exists a $f\in\mathcal{F}_{-\rho,\rho}(\mathbf{R}^{d})$ that interpolates $\{(x_{i},g_{i},f_{i})\}_{i\in I}$ and any global minimizer $x^\star$ of $f$ (i.e., $x^\star \in \textrm{argmin}_{x \in \mathbf{R}^d} f(x)$ ) is characterized by

f(x^\star) = f(x_{i^{\star}}-\frac{1}{L}g_{i^{\star}}) \leq f_{i^{\star}}-\frac{1}{2\rho}\|g_{i^{\star}}\|^{2}.\quad\quad\quad(3)

Proof to Theorem 4.

First, we prove $(ii)\Rightarrow(i)$ . If $(ii)$ holds, then obviously $f$ interpolates $\{(x_{i},g_{i},f_{i})\}_{i\in I}$ , hence $\{(x_{i},g_{i},f_{i})\}_{i\in I}$ is $\mathcal{F}_{-\rho,\rho}(\mathbf{R}^{d})$ -interpolable by Definition 1.

Next, we prove $(i)\Rightarrow(ii)$ . We want construct an interpolated function $f\in\mathcal{F}_{-\rho,\rho}(\mathbf{R}^{d})$ satisfying $(ii)$ . We have $\{(x_{i},g_{i},f_{i})\}_{i\in I}$ is $\mathcal{F}_{-\rho,\rho}(\mathbf{R}^{d})$ -interpolable, but due to Theorem 2, this is equivalent to saying $\{(x_{i},g_{i}+\rho x_{i},f_{i}+\frac{\rho}{2}\|x_{i}\|^{2})\}_{i\in I}$ is $\mathcal{F}_{0,2\rho}(\mathbf{R}^{d})$ -interpolable. Now, in Theorem 3, setting

\begin{aligned} \{(\widetilde{x}_{i},\widetilde{g}_{i},\widetilde{f}_{i})\}_{i\in I} & \coloneqq\{(x_{i},g_{i}+\rho x_{i},f_{i}+\frac{\rho}{2}\|x_{i}\|^{2})\}_{i\in I},\textrm{ and }\\ L & \coloneqq2\rho,\end{aligned}

we have the function $\widetilde{f}\in\mathcal{F}_{0,2\rho}(\mathbf{R}^{d})$ interpolating $\{(\widetilde{x}_{i},\widetilde{g}_{i},\widetilde{f}_{i})\}_{i\in I}$ defined by:

\begin{aligned} \widetilde{f}(y) & =\min_{\alpha\in\Delta}\left[\frac{L}{2}\|y-\sum_{i\in I}\alpha_{i}\left(\widetilde{x}_{i}-\frac{1}{L}\widetilde{g}_{i}\right)\|^{2}+\sum_{i\in I}\alpha_{i}\left(\widetilde{f}_{i}-\frac{1}{2L}\|\widetilde{g}_{i}\|^{2}\right)\right]\\ & =\min_{\alpha\in\Delta}\left[\rho\left\Vert y-\sum_{i\in I}\alpha_{i}\left(x_{i}-\frac{1}{2\rho}(g_{i}+\rho x_{i})\right)\right\Vert ^{2}+\sum_{i\in I}\alpha_{i}\left(f_{i}+\frac{\rho}{2}\|x_{i}\|^{2}-\frac{1}{4\rho}\|g_{i}+\rho x_{i}\|^{2}\right)\right],\end{aligned}

where $\Delta=\{\beta\in\mathbf{R}^{\vert I\vert}\mid\beta\geq0,\sum_{i\in I}\beta_{i}=1\}.$

Now, due to the proof $(ii)\Rightarrow(i)$ of Theorem 2, the function $f\coloneqq \widetilde{f}-(\rho/2)\|\cdot\|^{2}\in\mathcal{F}_{-\rho,\rho}(\mathbf{R}^{d})$ will interpolate $\{(x_{i},g_{i},f_{i})\}_{i\in I}$ . Hence, we have:

\begin{aligned} f(x) & =\widetilde{f}(x)-(\rho/2)\|x\|^{2}\\ & =\min_{\alpha\in\Delta}\left[\rho\left\Vert x-\sum_{i\in I}\alpha_{i}\left(x_{i}-\frac{1}{2\rho}(g_{i}+\rho x_{i})\right)\right\Vert ^{2}+\sum_{i\in I}\alpha_{i}\left(f_{i}+\frac{\rho}{2}\|x_{i}\|^{2}-\frac{1}{4\rho}\|g_{i}+\rho x_{i}\|^{2}\right)\right]-\frac{\rho}{2}\|x\|^{2}\\ & =\min_{\alpha\in\Delta}\left[-\frac{\rho}{2}\|x\|^{2}+\rho\left\Vert x-\sum_{i\in I}\alpha_{i}\left(x_{i}-\frac{1}{2\rho}(g_{i}+\rho x_{i})\right)\right\Vert ^{2}+\sum_{i\in I}\alpha_{i}\left(f_{i}+\frac{\rho}{2}\|x_{i}\|^{2}-\frac{1}{4\rho}\|g_{i}+\rho x_{i}\|^{2}\right)\right]\\ & =\min_{\alpha\in\Delta}\left[\frac{\rho}{2}\left\Vert x-\sum_{i\in I}\alpha_{i}\left(x_{i}-\frac{1}{\rho}g_{i}\right)\right\Vert ^{2}-\frac{\rho}{4}\left\Vert \sum_{i\in I}\alpha_{i}\left(x_{i}-\frac{1}{\rho}g_{i}\right)\right\Vert ^{2}+\sum_{i\in I}\alpha_{i}\left(f_{i}-\frac{1}{2\rho}\|g_{i}\|^{2}+\frac{\rho}{4}\left\Vert x_{i}-\frac{1}{\rho}g_{i}\right\Vert ^{2}\right)\right],\end{aligned}

where the last line follows from the following algebraic simplification (click to expand)

Hence, we have the interpolated function $f$ satisfying:

\begin{aligned} & f(x)\\ = & \min_{\alpha\in\Delta}\Big[\frac{\rho}{2}\|x-\sum_{i\in I}\alpha_{i}(x_{i}-\frac{1}{\rho}g_{i})\|^{2}-\frac{\rho}{4}\|\sum_{i\in I}\alpha_{i}(x_{i}-\frac{1}{\rho}g_{i})\|^{2}\\ & +\sum_{i\in I}\alpha_{i}(f_{i}-\frac{1}{2\rho}\|g_{i}\|^{2}+\frac{\rho}{4}\|x_{i}-\frac{1}{\rho}g_{i}\|^{2})\Big]\quad\quad\quad(4)\\ \overset{a)}{\geq} & \min_{\alpha\in\Delta}-\frac{\rho}{4}\left\Vert \sum_{i\in I}\alpha_{i}\left(x_{i}-\frac{1}{\rho}g_{i}\right)\right\Vert ^{2}+\sum_{i\in I}\alpha_{i}\left(f_{i}-\frac{1}{2\rho}\|g_{i}\|^{2}+\frac{\rho}{4}\left\Vert x_{i}-\frac{1}{\rho}g_{i}\right\Vert ^{2}\right)\\ \overset{b)}{\geq} & \min_{\alpha\in\Delta}-\frac{\rho}{4}\sum_{i\in I}\alpha_{i}\left\Vert x_{i}-\frac{1}{\rho}g_{i}\right\Vert ^{2}+\sum_{i\in I}\alpha_{i}\left(f_{i}-\frac{1}{2\rho}\|g_{i}\|^{2}+\frac{\rho}{4}\left\Vert x_{i}-\frac{1}{\rho}g_{i}\right\Vert ^{2}\right)\\ \overset{c)}{=} & \min_{\alpha\in\Delta}\cancel{-\frac{\rho}{4}\sum_{i\in I}\alpha_{i}\left\Vert x_{i}-\frac{1}{\rho}g_{i}\right\Vert ^{2}}+\sum_{i\in I}\alpha_{i}\left(f_{i}-\frac{1}{2\rho}\|g_{i}\|^{2}\right)+\cancel{\frac{\rho}{4}\sum_{i\in I}\alpha_{i}\left\Vert x_{i}-\frac{1}{\rho}g_{i}\right\Vert ^{2}}\\ = & \min_{\alpha\in\Delta}\sum_{i\in I}\alpha_{i}\left(f_{i}-\frac{1}{2\rho}\|g_{i}\|^{2}\right)\\ \overset{d)}{=} & \min_{i\in I}\{f_{i}-\frac{1}{2\rho}\|g_{i}\|^{2}\}\\ = & f_{i^{\star}}-\frac{1}{2\rho}\|g_{i^{\star}}\|^{2} \end{aligned}

where in $a)$ we construct a smaller term by removing the non-negative term $(\rho/2)\left\Vert x-\sum_{i\in I}\alpha_{i}\left(x_{i}-(1/\rho)g_{i}\right)\right\Vert ^{2}$ from the previous line, $b)$ uses Jensen's inequality

\|\sum_{i\in I}\lambda_{i}y_{i}\|^{2}\leq\sum_{i\in I}\lambda_{i}\|y_{i}\|^{2}:\textrm{where }\lambda\geq0,\sum_{i\in I}\lambda_{i}=1,

$c)$ just expands and cancels, and $d)$ uses the identity $\min_{i\in I}a_{i}=\min_{\alpha\in\Delta}\sum_{i\in I}\alpha_{i}a_{i}.$ So, we have shown that, for all $x\in\mathbf{R}^{d}$ we have

f(x)\geq f_{i^{\star}}-\frac{1}{2\rho}\|g_{i^{\star}}\|^{2},\quad\quad\quad(5)

i.e., $f_{i^{\star}}-(1/2\rho)\|g_{i^{\star}}\|^{2}$ is a global lower bound for the interpolated function $f$ . So, if we can show that some point $x^{\star}$ satisfies

f(x^{\star})\leq f_{i^{\star}}-\frac{1}{2\rho}\|g_{i^{\star}}\|^{2},

then $x^{\star}$ must be the global minimizer of $f$ . Now, if we set $\alpha\coloneqq e_{i^{\star}}$ ( $i^{\star}$ -th unit vector with its $i^{\star}$ -th component 1 and rest $0$ ) and $x\coloneqq x_{i^{\star}}-(1/\rho)g_{i^{\star}}$ in $(4),$ we have an upper bound of $f$ , i.e.,

\begin{aligned} & f(x_{i^{\star}}-(1/\rho)g_{i^{\star}})\\ = & \min_{\alpha\in\Delta}\Big[\frac{\rho}{2}\|x_{i^{\star}}-(1/\rho)g_{i^{\star}}-\sum_{i\in I}\alpha_{i}(x_{i}-\frac{1}{\rho}g_{i})\|^{2}-\frac{\rho}{4}\|\sum_{i\in I}\alpha_{i}(x_{i}-\frac{1}{\rho}g_{i})\|^{2}+\sum_{i\in I}\alpha_{i}(f_{i}-\frac{1}{2\rho}\|g_{i}\|^{2}+\frac{\rho}{4}\|x_{i}-\frac{1}{\rho}g_{i}\|^{2})\Big]\\ \leq & \Big[\frac{\rho}{2}\|x_{i^{\star}}-(1/\rho)g_{i^{\star}}-\sum_{i\in I}\alpha_{i}(x_{i}-\frac{1}{\rho}g_{i})\|^{2}-\frac{\rho}{4}\|\sum_{i\in I}\alpha_{i}(x_{i}-\frac{1}{\rho}g_{i})\|^{2}+\sum_{i\in I}\alpha_{i}(f_{i}-\frac{1}{2\rho}\|g_{i}\|^{2}+\frac{\rho}{4}\|x_{i}-\frac{1}{\rho}g_{i}\|^{2})\Big]_{\alpha=e_{i^{\star}}}\\ = & \frac{\rho}{2}\|\cancel{(x_{i^{\star}}-(1/\rho)g_{i^{\star}})}-\cancel{(x_{i^{\star}}-\frac{1}{\rho}g_{i^{\star}})}\|^{2}-\frac{\rho}{4}\|(x_{i^{\star}}-\frac{1}{\rho}g_{i^{\star}})\|^{2}+(f_{i^{\star}}-\frac{1}{2\rho}\|g_{i^{\star}}\|^{2}+\frac{\rho}{4}\|x_{i}-\frac{1}{\rho}g_{i}\|^{2})\\ = & \cancel{-\frac{\rho}{4}\|(x_{i^{\star}}-\frac{1}{\rho}g_{i^{\star}})\|^{2}}+(f_{i^{\star}}-\frac{1}{2\rho}\|g_{i^{\star}}\|^{2})+\cancel{\frac{\rho}{4}\|x_{i}-\frac{1}{\rho}g_{i}\|^{2}}\\ = & f_{i^{\star}}-\frac{1}{2\rho}\|g_{i^{\star}}\|^{2}\quad\quad\quad(6).\end{aligned}

So the lower bound on $f$ in $(5)$ is achieved by $x_{i^{\star}}-(1/\rho)g_{i^{\star}}$ . Hence, any global minimizer $x^\star$ of $f$ (i.e., $x^\star \in \textrm{argmin}_{x \in \mathbf{R}^d} f(x)$ ) is characterized by

f(x^\star) = f(x_{i^{\star}}-\frac{1}{L}g_{i^{\star}}) \leq f_{i^{\star}}-\frac{1}{2\rho}\|g_{i^{\star}}\|^{2},

and this completes the proof ■

References

[1] Drori, Y., & Shamir, O. (2020, November). The complexity of finding stationary points with stochastic gradient descent. In International Conference on Machine Learning (pp. 2658-2667). PMLR. Link

[2] Adrien B Taylor, Julien M Hendrickx, and Fran¸cois Glineur. Exact worst-case performance of first-order methods for composite convex optimization. SIAM Journal on Optimization, 27(3):1283–1313, 2017. Link

[3] Taylor, Adrien B. Convex interpolation and performance estimation of first-order methods for convex optimization. Diss. Catholic University of Louvain, Louvain-la-Neuve, Belgium, 2017. Link

[4] Drori, Yoel. The exact information-based complexity of smooth convex minimization. Journal of Complexity 39 (2017): 1-16. Link

Lemma 1: Relation between smooth convex and nonconvex functions. Lemma

Definition 1: Interpolable function. Definition

Theorem 1: Interpolation condition for smooth nonconvex functions. Theorem

Theorem 2: Minimal curvature addition and interpolation. Theorem

Theorem 3: Interpolation of smooth convex functions. Theorem

Theorem 4: Properties of interpolated function for smooth nonconvex function class Theorem